Community
Broccoli, Funny Fish and the Universe: the Beauty of Math Hidden in Everyday Life
l
NM
By Nathália M on April 11, 2025
I’m sure you’ve heard your teacher mention how “math is everywhere”. They were probably talking about the supermarket, or the movies, or maybe your Schoolhouse tutor even mentioned the math you might use in a STEM career. Prices, bills, time…all everyday instances of numbers, ever-present yet something we almost pay no mind to.
Physical nature and mathematics can connect in truly mesmerizing ways, way beyond the equations in our math exams, and this post will give you a glimpse of this new side of “everywhere” math.
Let’s find out what broccoli or fish has to do with any of this, and get into some curious instances of these unforgettable connections: patterns.
Simply put, patterns are everything that repeats in a predictable manner. Mathematics is, many times, the tool we can use to predict these repeating structures, often described by models and formulas constantly perfected and reformulated to describe real life and the universe as accurately as humanly possible.
The Golden Ratio
The Golden Ratio is a classic. It was defined by the Greek mathematician Euclid as the ratio between two consecutive line segments A and B such that (A+B)/A = A/B. As you progress through the Fibonacci Sequence (the one where you start with 1 and add the previous number to get the next: 1, 1, 2, 3, 5, 8, 13…), the ratio between two consecutive numbers gets closer and closer to the Golden Ratio:
The Golden Ratio
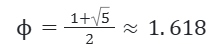
The Golden Spiral
The Golden Spiral, a pattern inscribed in a set of squares and rectangles proportional to the Golden Ratio, is known to be present everywhere, from seed heads to ancient architecture. In a sunflower, for example, the angle between successive seeds approximates the Golden Angle, about 137.5 degrees, which is also derived from the Golden Ratio.
There is a problem, though, when it comes to the Golden Ratio’s claimed relation to perfect beauty. For the human face, for example, the idea that a perfect face is proportional to the Golden Ratio is a complete myth (a bummer, I know), just like proportions in Greek architecture do align with the Golden Ratio, while claims about this specific proportion’s link to pleasing aesthetics can be very subjective and misleading.
If you are ever tempted to rearrange your school supplies in your desk based on the Golden Ratio, or critique a painting for not adhering to its principles, remember that while it's a fascinating mathematical concept, it's not the magic key to aesthetic perfection (unless, of course, you're a sunflower seed head, in which case, spiral away, you astoundingly mathematical being!).
Fractals
Now, if the Golden Ratio could be the supermodel of math patterns, fractals would be the rebellious artists. Take a shape: maybe a triangle, or a squiggle. Now, take that shape and shrink it down, make a bunch of copies, and arrange them in the same pattern as the original shape. Then, do it again. And again. And again. This is basically the structure of a fractal. It's like those Russian nesting dolls, but with math!
And like many mathematical patterns, these infinite, self-similar wonders can be found everywhere! Think broccoli, specifically Romanesco broccoli, the psychedelic cousin of your standard green flower (yup, broccoli is a flower!), or snowflakes, each one a unique, frozen fractal masterpiece. Coastlines, river networks, even the branching patterns of our lungs – all fractals! It's as if the universe decided to play a never-ending game of copy-paste, and honestly, who are we to complain? Just don't get lost trying to zoom in forever on a fractal, you might find yourself questioning the nature of reality (and miss your Schoolhouse session).
Turing Patterns
Though less well known, Turing patterns create some of the most intriguing structures out there, and they are present in so many more places than you think!
Alan Turing, the father of computer science, was also an avid theoretical biologist, and his timeless paper “The Chemical Basis of Morphogenesis” took academia by storm with it’s surprisingly accurate model describing what we know today as Reaction-Diffusion systems, responsible for mapping the way those funny stripes in animal skins, seashells and even watermelons form.
We start with two hypothetical chemicals, an activator and an inhibitor. The activator promotes the production of itself and the inhibitor, while the inhibitor suppresses the activator's production, both chemicals spreading through a medium (an animal’s skin, sand dunes, you name it) at different rates.
From the regular spacing of hair follicles to the way our blood vessels form and spread, even our body has all sorts of ways to surprise us with math, as these are also thought to be influenced by reaction-diffusion mechanisms!
Conclusion
So, next time you’re at the supermarket and begin to wonder why the cereal costs $4.99 instead of $5.00, remember there are many more mathematical wonders to investigate beyond our everyday endeavors. Maybe shift your focus to the Romanesco Broccoli by the other aisle and take your time appreciating the wonders of fractals, or perhaps ponder the chemical reactions that helped create the stripes of the watermelons a couple shelves ahead.
Sources:
- https://www.salon.com/2021/02/09/what-makes-romanesco-broccoli-so-mathematically-perfect/
-
https://owlcation.com/stem/Astounding-Ways-How-Mathematics-is-a-Part-of-Nature-
